전 게시글에 이어서 사과, 파인애플, 바나나 사진을 가지고 하겠습니다.
만약, 비지도 학습에서 각 과일의 평균을 구하라고 하면 구할 수 있을까요?
정답은 "할 수 없습니다" 입니다.
왜냐하면 어떤 사진에 어떤 과일이 있을지 모르기 때문입니다.
그렇다면 어떻게 평균값을 구할 수 있을까요?
k-평균(K-Means)
k-평균(K-Means) 군집 알고리즘은 평균값을 자동으로 찾아줍니다.
이 평균값이 클러스터 중심에 위치하기 때문에 클러스터 중심(cluster center) 또는 센트로이드(centroid)라고 부릅니다.
k-평균 알고리즘의 작동 방식은 다음과 같습니다.
1. 무작위로 k개의 클러스터 중심을 정한다.
2. 각 샘플에서 가장 가까운 클러스터 중심을 찾아 해당 클러스터의 샘플로 지정한다.
3. 클러스터에 속한 샘플의 평균값으로 클러스터 중심을 변경한다.
4. 클러스터 중심에 변화가 없을 때까지 2번으로 돌아가 반복한다.
그럼 이제 사이킷런으로 k-평균 모델을 만들어보겠습니다.

저번과 같은 데이터이고, (샘플 개수, 너비, 높이) 크기의 3차원 배열입니다.
이것을 저희는 (샘플 개수, 너비 x 높이) 크기를 가진 2차원 배열로 변경했습니다.
이제 클래스를 구현해보겠습니다.

사이킷런의 k-평균 알고리즘은 sklearn.cluster 모듈에서 KMeans 클래스에 구현되어 있습니다.
그리고 클러스터 개수를 지정하는 n_clusters에는 3개로 지정되어 있습니다.
여기서 fit() 메서드를 보면 타깃 데이터를 사용하지 않고 있습니다.
이는 비지도 학습이기 때문입니다.
이제 군집 결과를 한번 살펴보겠습니다.
결과는 KMeans 클래스 객체의 labels_ 속성에 저장됩니다.
labels_ 배열의 길이는 샘플 개수와 같고, 이 배열은 각 샘플이 어떤 레이블에 해당되는지 나타냅니다.
현재 n_clusters = 3으로 지정되어 있기 때문에 배열의 값은 0, 1, 2 중 하나입니다.

레이블값과 레이블 순서는 의미가 없습니다.
레이블 0, 1, 2로 모은 샘플의 개수도 확인해보겠습니다.

첫 번째 클러스터(레이블 0)은 111개의 샘플을 모았고, 두 번째 클러스터(레이블 1)가 98개의 샘플을 모았습니다.
그리고 세 번째 클러스터(레이블 2)는 91개의 샘플을 모았습니다.
그럼 한번 각 클러스터가 어떤 이미지를 나타내는지 간단한 함수를 만들고 확인해보겠습니다.

함수를 사용하되 불리언 인덱싱 방식으로 각 클러스터에 해당되는 이미지를 출력해보겠습니다.

레이블 0으로 된 클러스터는 파인애플이고, 사과 9개와 바나나 2개가 섞여 있습니다.
나머지도 한번 살펴보겠습니다.


레이블 1과 레이블 2는 사과와 바나나였습니다.
훈련 데이터에 타깃 레이블을 사용하지 않고도 어느정도 분류된 것을 확인할 수 있습니다.
클러스터 중심
KMeans 클래스가 최종적으로 찾은 클러스터 중심은 cluster_centers_ 속성에 저장되어 있습니다.
이 배열은 fruits_2d 샘플의 클러스터 중심이기 때문에 이미지로 출력하려면 100 x 100 크기의 2차원 배열로 바꿔야 합니다.

KMeans 클래스는 훈련 데이터 샘플에서 클러스터 중심까지 거리로 변환해 주는 tranform() 메서드가 있습니다.
이는 특성값을 변환하는 도구로 사용할 수 있다는 의미와 같습니다.
그럼 한번 인덱스가 100인 샘플에 transform() 메서드를 적용해보겠습니다.
마찬가지로 이 메서드도 2차원 배열을 넣어야 합니다.

첫 번째 값이 레이블 0, 두 번째 값이 레이블 1, 세 번째 값이 레이블 2입니다.
레이블 0까지의 거리가 3393.8로 가장 작습니다. 그렇다면 이 샘플은 레이블 0에 속하는 것 같습니다.
한번 predict() 메서드로 확인해보겠습니다.

transform() 결과에서 예상한 것과 같게 레이블 0으로 예측했습니다.
레이블 0은 파인애플이였는데 그림도 확인해보겠습니다.

k-평균 알고리즘은 앞에서 설명했듯이 반복적으로 클러스터 중심을 옮기면서 최적의 클러스터를 찾습니다.
알고리즘이 반복한 횟수는 KMeans 클래스의 n_iter_ 속성에 저장됩니다.

최적의 k 찾기
k-평균 알고리즘의 단점 중 하나는 클러스터 개수를 사전에 정해야 한다는 것입니다.
실전에서는 몇 개로 해야 할지 정해져 있지 않기 때문에 어려움을 느낄 수 있습니다.
사실 군집 알고리즘에서 적절한 k 값을 찾는 완벽한 방법은 존재하지 않습니다.
대신 몇 가지 도구가 있습니다.
이 도구들은 각자 장단점이 존재합니다.
이 중 저희는 엘보우(Elbow) 방법에 대해 알아보겠습니다.
앞에서 본 것처럼 k-평균 알고리즘은 클러스터 중심과 클러스터에 속한 샘플 사이의 거리를 잴 수 있습니다.
이 거리의 제곱 합을 이너셔(Inertia)라고 부릅니다.
이너셔는 클러스터에 속한 샘플이 얼마나 가깝게 모여 있는지를 나타내는 값입니다.
일반적으로 클러스터 개수가 증가하면 클러스터 개개의 크기는 작아지기 때문에 이너셔도 줄어듭니다.
엘보우 방법은 클러스터 개수를 늘려가면서 이너셔의 변화를 관찰하여 최적의 클러스터 개수를 찾는 방법입니다.
클러스터 개수를 증가시키면서 이너셔를 그래프로 그리면 감소하는 속도가 꺾이는 지점이 있습니다.
이 지점부터는 클러스터 개수를 늘려도 클러스터에 잘 밀집된 정도가 크게 개선되지 않습니다.
이 말은 즉, 이너셔가 크게 줄어들지 않습니다.
이 모습이 마치 팔꿈치 모양이라서 엘보우 방법이라 불립니다.
그럼 한번 계산해보겠습니다.
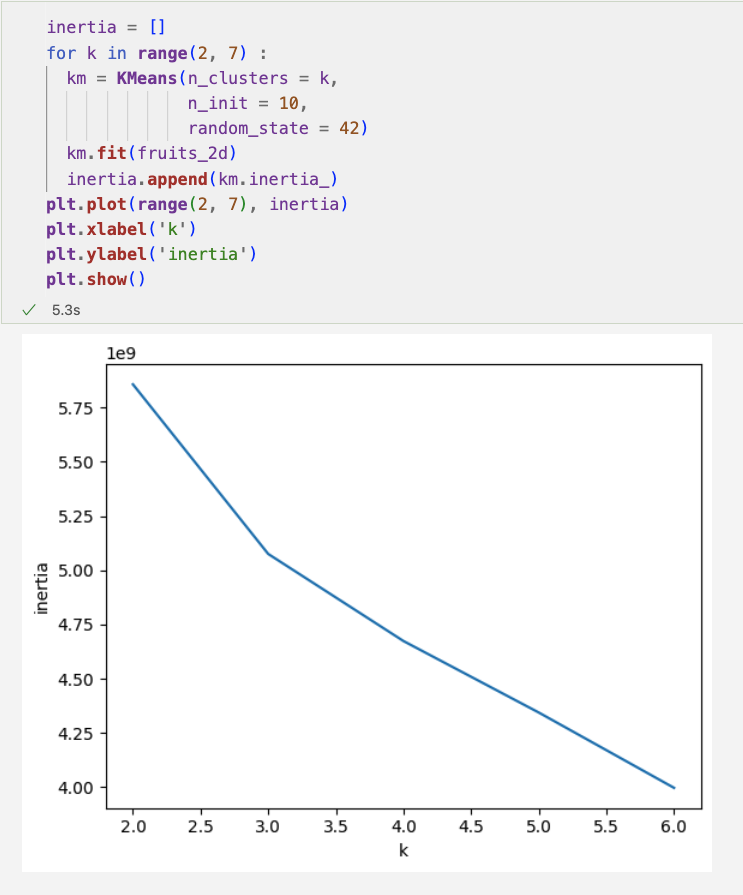
코드를 살펴보면
클러스터 개수를 2에서 6까지 바꿔가며 KMeans 클래스를 5번 훈련하고
inertia_ 속성에 저장된 이너셔 값을 순서대로 리스트에 추가했습니다.
이 그래프에서는 꺾이는 지점이 뚜렷하지는 않지만, k = 3에서 그래프의 기울기가 조금 바뀐 것을 볼 수 있습니다.
출처 : 혼자 공부하는 머신러닝 + 딥러닝
https://product.kyobobook.co.kr/detail/S000001810330
다음 장에서는 주성분 분석에 대해서 알아보겠습니다.
'Study > 혼자 공부하는 머신러닝 + 딥러닝' 카테고리의 다른 글
| [혼자 공부하는 머신러닝 + 딥러닝] 주성분 분석 (0) | 2024.12.02 |
|---|---|
| [혼자 공부하는 머신러닝 + 딥러닝] 군집 알고리즘 (0) | 2024.11.13 |
| [혼자 공부하는 머신러닝 + 딥러닝] 트리의 앙상블 (1) | 2024.11.11 |
| [혼자 공부하는 머신러닝 + 딥러닝] 교차 검증과 그리드 서치 (0) | 2024.11.07 |
| [혼자 공부하는 머신러닝 + 딥러닝] 결정 트리 (0) | 2024.10.31 |



